
Consideriamo il quadrilatero ABCD con i lati e gli angoli congruenti:
AB = BC = CD = DA
A = B = C = D
Questo quadrilatero regolare si chiama quadrato.
Pertanto:
Si chiama quadrato un parallelogrammo che ha i lati congruenti e gli angoli congruenti.
Ora siccome la somma degli angoli interni di un quadrilatero è di 360°, si ha che ogni angolo di ABCD è retto:
A = B = C = D = 90°
Il quadrato è quindi:
- Un particolare rettangolo perché ha gli angoli congruenti e retti.
- Un particolare rombo perché ha i lati congruenti.
E' evidente che tutte le proprietà dei rettangoli e dei rombi valgono anche per i quadrati, in particolare possiamo affermare che:
Le diagonali di un quadrato sono congruenti e perpendicolari:
AC = BD; AC ⊥ BD
Anche in questo caso vale la proprietà inversa, cioè:
se un parallelogrammo ha le diagonali congruenti e perpendicolari è un quadrato.
Anche in questo caso vale la proprietà inversa, cioè:
se un parallelogrammo ha le diagonali congruenti e perpendicolari è un quadrato.
Formule del Quadrato dirette e inverse
L = lato;
A = area;
d = diagonale;
2p = perimetro.
A = area;
d = diagonale;
2p = perimetro.
| Area |  |
| Area |  |
| Area | 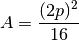 |
| Lato |  |
| Lato |  |
| Lato |  |
| Diagonale | 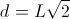 |
| Diagonale |  |
| Perimetro |  |
| Perimetro | 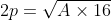 |
| Perimetro |  |
GUARDATE ANCHE: Problemi sul Quadrato












