Un rombo ha l'altezza lunga 2,5 cm e un angolo acuto è ampio 45°. Calcola:
la lunghezza del perimetro del rombo; l'area del rombo; la lunghezza del lato e l'area di un quadrato avente la diagonale lunga come il perimetro del rombo.
Svolgimento:
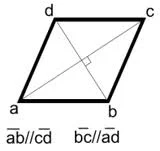
Se dividiamo il rombo in 4 otteniamo 4 triangoli rettangolo. Che hanno un angolo di 90° e due angoli acuti di 45°.
Adesso, non mi ricordo come si fa esattamente ma c'è questa formula ed avendo i 3 angoli a disposizione puoi calcolarti l'area.
A = B = C = D = 45°
O = 90°


la lunghezza del perimetro del rombo; l'area del rombo; la lunghezza del lato e l'area di un quadrato avente la diagonale lunga come il perimetro del rombo.
Svolgimento:
Se dividiamo il rombo in 4 otteniamo 4 triangoli rettangolo. Che hanno un angolo di 90° e due angoli acuti di 45°.
Adesso, non mi ricordo come si fa esattamente ma c'è questa formula ed avendo i 3 angoli a disposizione puoi calcolarti l'area.
A = B = C = D = 45°
O = 90°


Dopo che ti sei calcolata l'area, con la formula inversa ti devi trovare il lato.
l = A / h
Per calcolarti il perimetro del rombo devi moltiplicare il lato per 4.
P = l x 4
QUADRATO
Adesso invece tocca al quadrato. Con il perimetro appena calcolato sei a conoscenza del valore della diagonale del quadrato.
d = P
Con la formula qui in basso ti trovi l'area.

Per calcolare il lato del quadrato devi fare la radice quadrata dell'area.
√A = l
In questo modo l'esercizio è risolto. Purtroppo per te non mi ricordo le regole e le formule sugli angoli ma risolvendo la prima formula sugli angoli (forse la più complessa) per il resto devi semplicemente sostituire alle formule che ho scritto i dati del tuo problema.












